1.“不同表示方法表示同种图形的面积”可以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法,
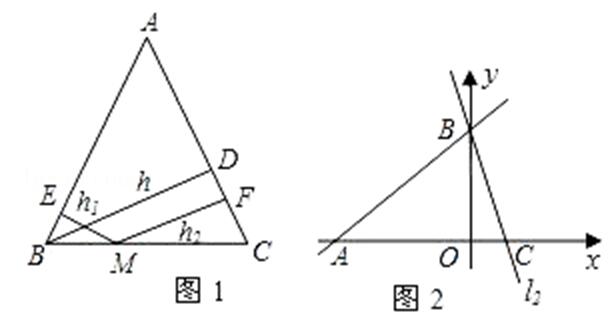
(1)如图1,在等腰三角形ABC中,AB=AC,AC边上的高为h,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为h1、h2,请用面积法证明:h1+h2=h;
(2)当点M在BC的延长线上时,h1、h2、h之间的等量关系式是什么?
(3)如图2,在平面直角坐标系中有两条直线l1:y=(3/4)x+3,l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,请运用(1)(2)的结论求出点M的坐标.
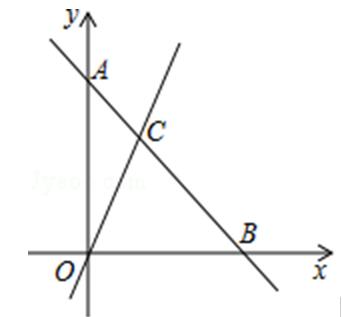
2.如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O→C→B运动.
(1)求直线AB的解析式;
(2)当△OPB的面积是△OBC的面积的时(1/4),求出这时点P的坐标;
(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.

我的微信
微信号已复制
遇见数学-微信公众号
善不由外来兮,名不可以虚作。做有情怀的教育。

